Aggregated model

from prayas import *

The experiment consists of multiple variants and in each variant the visitor has one ore more options to choose, but we only observe the overall success. A detailed explanation of the methodology is available in Bayesian A/B Testing for Business Decisions by Shafi Kamalbasha and Manuel J. A. Eugster (2020).

This data is the same as for the multi-option model – the experiment consists of two variants with each variant having 9 different options from which the visitor can choose. However, we are going to simulate that we are only observing the aggregated measures. The model is setup as:

m = AggregateModel(variants=["Original", "Progressive"],
                   baseline="Original")

To simulate the aggregated observations, we sum up the measures also used in the multi-option model example:

# Revenue of the 9 options per variant:
rev_a = [27.95,  47.95,  63.95,
         35.95,  63.95,  79.95,
         79.95, 151.95, 223.95]
rev_b = [34.95,  59.95,  79.95,
         37.95,  67.95,  84.95,
         69.95, 132.95, 195.95]

# Conversions of the 9 options per variant:
conv_a = [50, 5, 5, 28, 7, 5, 20, 1, 6]
conv_b = [28, 3, 6, 30, 6, 5, 27, 6, 3]

# Aggregates:
totals_rev_a = np.sum([a*b for a, b in zip(rev_a, conv_a)])
totals_rev_b = np.sum([a*b for a, b in zip(rev_b, conv_b)])

totals_conv_a = np.sum(conv_a)
totals_conv_b = np.sum(conv_b)

Compared to the one option model and the multi-option model, the measures are also an outcome of the experiment and set together with the result:

m.add_measure("revenue", [totals_rev_a, totals_rev_b])
m.add_measure("gain", [totals_rev_a, totals_rev_b], [-0.06*9, -0.04*9])

m.set_result([totals_conv_a, totals_conv_b], [8067, 8082])

Investigate the result:

m.plot();

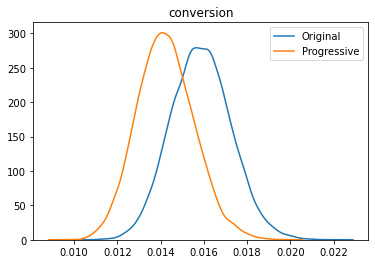
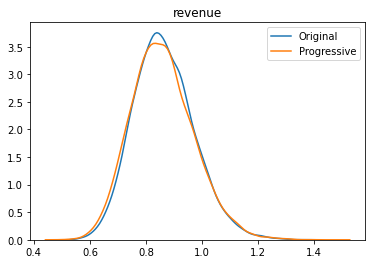
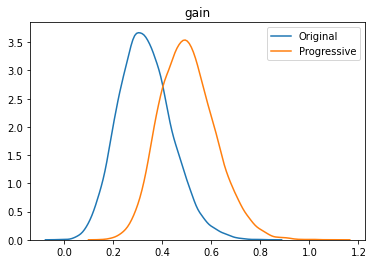
Get details on the result:

m.score_baseline()

	Variant	Measure	ProbabilityToBeBest	ProbabilityToBeatBaseline	UpliftFromBaseline	PotentialLossFromBaseline	MaxUplift	MaxPotentialLoss
0	Progressive	gain	0.87150	0.86545	51.823793	3.276094	52.106298	3.219060
1	Original	conversion	0.79955	0.00000	0.000000	0.000000	11.428042	1.462822
2	Original	revenue	0.51010	0.00000	0.000000	0.000000	0.504426	7.058403
3	Progressive	revenue	0.48990	0.49145	-0.554503	7.391586	-0.501895	7.456368
4	Progressive	conversion	0.20045	0.19300	-10.361264	11.665751	-10.255984	11.554384
5	Original	gain	0.12850	0.00000	0.000000	0.000000	-34.256503	36.409115

The comparison with the multi-options model shows a similar result.